Spiking Neurons
Some types of neuron update rules produce discrete “spikes” (instantaneous firing events). When they do, the neuron and the lines leading out from it (the “axon”) turn a different color (by default yellow). This framework is used to create more biologically realistic simulations. In these models, activation (the number shown in the neuron) is usually interpreted as a voltage potential, and when that number passes a threshold the neuron “fires,” and sends a signal to other neurons.
Since spikes are discrete events without a numerical value, some way of converting them into numbers is required when a spike arrives at a synapse. This is handled using spike responders.
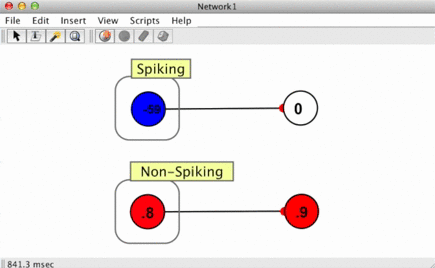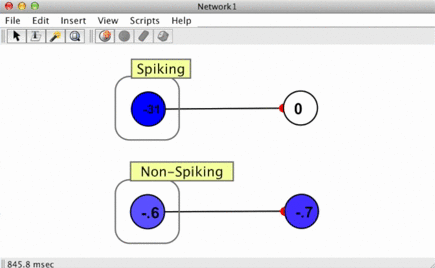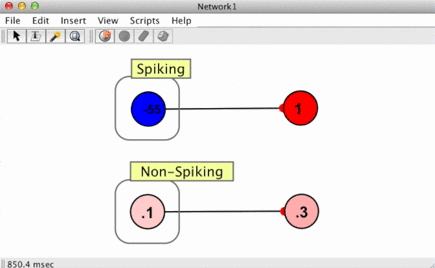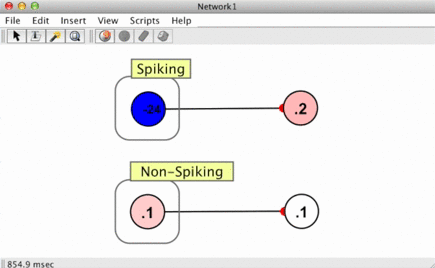
To see how different spike responders produce different PSR shapes, try the spiking neuron simulation (Simulations > Neuroscience > Spiking Neuron).
Visualizing Spikes
When synapses are visible in the network panel, they turn yellow when their source neuron spikes, creating a visual effect that makes it easy to see signal propagation through the network (To see spikees in action, try the spiking network simulation (Simulations > Neuroscience > Spiking Network). However, displaying many synapses can slow down the simulation.
For better performance while still observing spike activity, you have several options:
- Toggle synapse visibility: Press
5or useView > Free Weights Visibleto hide synapses entirely. This significantly improves performance in large networks. - Show only when spiking: Enable Only show synapses when spiking to hide synapses by default and only display them briefly when they transmit a spike. This provides an intermediate option between full visibility and complete hiding.
See the network menus page for more visibility options.
Spike Timing / Implementation Notes
When a spiking neuron fires, two key pieces of information are tracked:
- Spike state: A boolean indicating whether the neuron spiked in the current time step
- Last spike time: The simulation time when the neuron most recently spiked
The last spike time is initialized to negative infinity, indicating the neuron has never spiked. This value is updated each time the neuron fires and is used by learning rules like STDP to calculate spike timing differences.
You can access spike information in scripts:
if (neuron.isSpike) {
println("Neuron spiked at time ${neuron.lastSpikeTime}")
}
For neuron arrays, spike data is stored as arrays that can be accessed through the array’s data holder.
Historical Comments
Historically, there has been a progression from one-dimensional (1D) to two-dimensional (2D) neuron models.
Hodgkin-Huxley is the original model, which is quite complex, involving four or five state variables.
Integrate-and-Fire is a simpler model, often 1D, though some versions extend to 2D.
FitzHugh-Nagumo was designed as a simplification of the Hodgkin-Huxley model. This 2D dynamical system captures much of the variability and behavior seen in Hodgkin-Huxley. It effectively models voltage traces and spike timings, demonstrating that simpler models can approximate the more complex original.
Following these models, there were attempts to not only model voltage traces but also capture spike dynamics and timings using 2D simplifications. These models can reproduce bursting behavior. The second variable in these models usually represents some form of adaptation.
Spike Timing Emphasis
Models with a spike timing emphasis aim to reproduce accurate spike timings and realistic voltage traces. They are designed to diverge to infinity, a feature of their construction. Examples include Izhikevich, Integrate-and-Fire, Adaptive Exponential Integrate-and-Fire (AdEx), and Morris-Lecar.
AdEx is considered a gold standard for spike timing. It excels at predicting when spikes will occur in response to input and can produce realistic voltage traces. However, these are unstable dynamical systems, often requiring “reset” mechanisms to handle divergence. Among these models, AdEx is the best at predicting the exact timing of spikes after an input, whereas Izhikevich and quadratic Integrate-and-Fire models may not diverge to infinity quickly enough, resulting in delayed spikes. IntFire models, on the other hand, may produce spikes too soon.
Membrane Trace Emphasis
Models focusing on membrane potential traces include FitzHugh-Nagumo, Hodgkin-Huxley, and Morris-Lecar. These models are good at producing accurate voltage traces and do not diverge to infinity. Instead, they treat spikes as certain values and reset afterward.
These models include recovery variables that simulate the depletion and replenishment of certain chemicals in the neuron. After reaching a threshold, sodium ions rush into the cell, and the gradient diffusion follows an exponential curve, initially rapid but then saturating as equilibrium is approached. This process is not limited by the depletion of ions but by the rate at which they can be replenished. The response to this saturation often involves the opening of calcium channels, allowing calcium ions to exit the cell. The energy expended is primarily in resetting the neuron rather than firing the spike itself, often involving active pumps.
Morris-Lecar is closely related to FitzHugh-Nagumo and focuses on modeling calcium dynamics. It can generate accurate voltage traces without directly modeling sodium dynamics. FitzHugh-Nagumo models ion saturation effects, particularly sodium, and captures the general behavior of ion influx and efflux.
Background Currents
Without some background current, a neuron requires a significant amount of input to reach the threshold needed to fire a spike, which is unrealistic. Excessive input can push the neuron into an unstable state, leading to seizure-like activity.
Neurons naturally maintain a sub-threshold excited state due to the averaged activity from other neurons. This background activity keeps them close to the boundary between quiescence and excitability, facilitating synaptic transmission.
Avoiding Instability
Some tips to avoid instability in neuron models:
- The time step should be small, but 0.1 is usually sufficient.
- Be careful with time constants: they must be positive and non-zero.
- The time constant should be significantly larger than the time step. Lower time constants increase instability; values below 1 can be particularly problematic. Ideally, the time constant should be at least 10.
- A time constant of around 3 is acceptable for spike responders, as neurotransmitters are quickly cleared from the synaptic cleft, ensuring transmission. The rise and decay of these signals require careful consideration.
List of Spiking Neurons
The following spiking neuron update rules are available in Simbrain: