Competitive Group

A competitive group is a collection of neurons that compete with each other to represent clusters of inputs. With training, the nodes come to represent particular clusters of inputs, making them useful for unsupervised learning and pattern classification.

The competitive group combines elements of winner-take-all networks and Hebbian learning. The self-organizing map is a spatial generalization of this algorithm.

The simple competitive learning algorithm implemented here serves as a toy model that illustrates how neural networks in the brain might perform clustering. The algorithm identifies a winning neuron based on which has the highest activation to a given input, then adjusts only that neuron’s weights to better match the input pattern. Over time, different neurons become specialized to respond to different clusters of input patterns, with each neuron’s fan-in weight vector migrating toward the center of its associated input cluster. In machine learning contexts, similar clustering objectives are often achieved using algorithms like k-means clustering. The competitive network provides a biologically inspired alternative that demonstrates how such clustering might emerge through neural competition and learning.

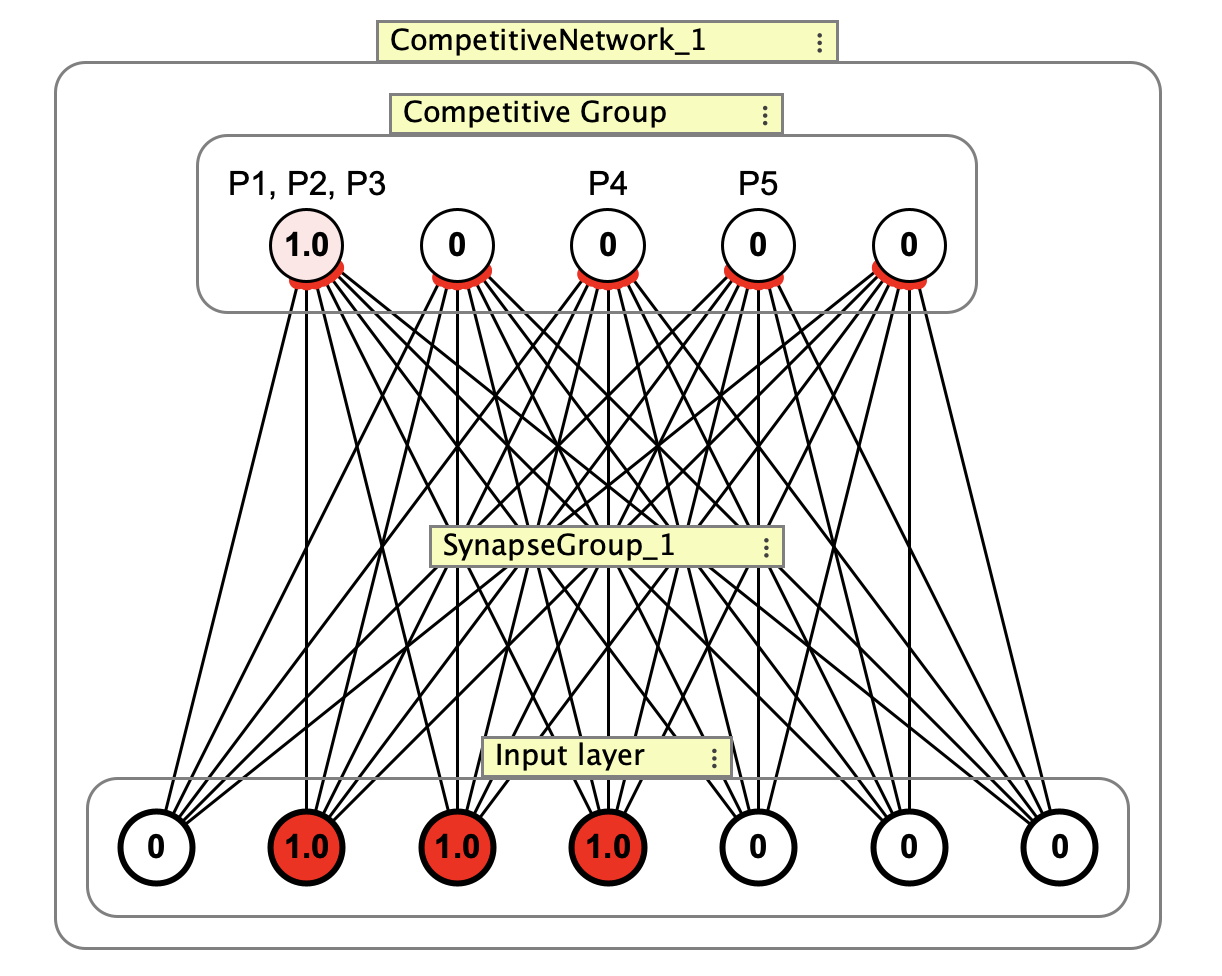
From the Simulations > Competitive > Competitive network (simple) simulation. This network has been trained on patterns P1-P5 and currently cannot distinguish P1-P3.

A competitive group may be used standalone (connected to other neurons by the user) or as part of a pre-configured competitive network that includes an input layer and training interface.

Algorithm

The basic algorithm described here is the original PDP version due to Rumelhart and Zipser. An alternative, due to Alvarez and Squire, is also available (see references below).

1. Compute the weighted input to every unit.
2. Determine the winner, which is the unit with the greatest weighted input. In the case of a tie, this is done arbitrarily.
3. Update the weights attaching to the winning neuron only. These weights are changed by the following quantity: learning rate times the source activation divided by the total activation of the source layer minus the current strength of the weight:

\[\Delta w = \epsilon \left( \frac{a_i}{\sum a_{inputs}} - w_{ij} \right)\]

where \(\epsilon\) is a learning rate, \(\sum a_{inputs}\) is the sum of all the inputs to the unit, and \(a_i\) is an input neuron’s activation. This algorithm has the result that the winning unit’s weights come over time to resemble the input vector that led that unit to win. The learning rate controls how quickly this happens.

The division by the sum of inputs maintains the normalization of the weight vectors. Thus, if more strength is added to one weight, it is taken away from another.

Leaky Learning

A variant of the competitive learning algorithm called leaky learning requires all weights to learn on each time step, rather than just the winning weight. The algorithm for the weight change on the losing units is the same as above, but a new learning rate parameter is used, which will typically be smaller than the winning unit learning rate, so that weights attaching to losing neurons learn more slowly.

Parameters

• Update method: Select either Rummelhart-Zipser (the classic PDP algorithm described above) or Alvarez-Squire (see references).
• Learning rate: Determines how quickly synapses change during training.
• Winner Value: The activation value for the winning neuron.
• Lose Value: The activation value for all losing neurons.
• Normalize inputs: If enabled, inputs are normalized prior to being used in weight updates.
• Use Leaky learning: If enabled, all weights learn on each time step, not just the weights attaching to the winning unit.
• Leaky learning rate: The learning rate for losing neurons when leaky learning is enabled. Only visible when Use Leaky learning is checked.
• Decay percent: Amount to decay incoming synapses at every iteration. Only used with the Alvarez-Squire update method. Only visible when Alvarez-Squire is selected.

Right Click Menu

Generic right-click items are described on the neuron group page.

• Edit / Train Competitive: Opens edit dialog to edit and train the competitive group.
• Randomize Synapses: Randomize synapses connected to the competitive group.

References

The Rumelhart and Zipser update rule is described in this PDP handbook chapter. Also see the PDP volumes, volume 1, chapter 5.

The Alvarez and Squire version of the algorithm is described in this PNAS paper.